Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема 3. ВОЛНОВЫЕ СВОЙСТВА МИКРОЧАСТИЦ ВЕЩЕСТВА 3.1. Гипотеза де Бройля 3.2
Содержание
- 1. Тема 3. ВОЛНОВЫЕ СВОЙСТВА МИКРОЧАСТИЦ ВЕЩЕСТВА 3.1. Гипотеза де Бройля 3.2
- 2. 3.1. Гипотеза де Бройля х Появилась необходимость пересмотра
- 3. х В 1924 г. Луи де Бройль выдвинул
- 4. хЛуи де Бройль (1892 – 1987), французский
- 5. х «В оптике, – писал де Бройль, –
- 6. х Если фотон обладает энергией E=hv и импульсом
- 7. Согласно квантовой механике, свободное движение
- 8. х При взаимодействии частицы с
- 9. х Гипотеза де Бройля
- 10. х3.2. Дифракция частиц Дифракция частиц - рассеяние
- 11. х Первым опытом по дифракции частиц, блестяще подтвердившим
- 12. "Некоторые исследователи -Дэвисон и Джермер и молодой
- 13. для наблюдения за ихдушевным состоянием.Но они добилисьу с п е х а !"
- 14. Эти опыты показали, что в определенных условиях
- 15. Ni монокристаллпики дифракциипоток электронов В опыте Дэвиссона и
- 16. Эти максимумы отражённых пучков электронов соответствовали условию
- 17. х При высоких ускоряющих напряжениях (десятках кВ) электроны
- 18. В 1949 г. советские ученые Л.М. Биберман,
- 19. х Вскоре после этого удалось наблюдать и явления
- 20. х Для лёгких атомов
- 21. х Сформированный с помощью диафрагм молекулярный или атомный
- 22. х Позже наблюдалась дифракция протонов, а также дифракция
- 23. Позднее была обнаруженадифракция протонов, нейтронов,и атомов водорода.
- 24. Картина дифракции электронов на слюде
- 25. Картина дифракции нейтронов на кварце
- 26. Это означает, что волновыесвойства присущи всем частицам микромира.
- 27. х Дифракция частиц, сыгравшая в своё время столь
- 28. х3.3. Корпускулярно- волновойдуализм микрочастиц вещества Итак, микрочастицы
- 29. Микрочастицы не способны непосредственно воздействовать на
- 30. х В доквантовой физике понять - значить составить
- 31. х Рассмотренные нами волны де Бройля не являются
- 32. х Дебройлевская длина волны обычного тела слишком мала,
- 33. х Другое дело, если речь идет об элементарных
- 34. х Из приведенного примера видно, что электрон может
- 35. Тема 4. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ 4.1. Соотношение неопределенностиГейзенберга4.2. Понятие о волновой функциих4.3. Уравнение Шредингера
- 36. х4.1. Соотношение неопределенности Гейзенберга Согласно двойственной корпускулярно-волновой
- 37. Корпускулярно-волновая двойственность свойств частиц, изучаемых в
- 38. хИз уравнения следует, что чем меньше неопределенность
- 39. Соотношение неопределенностей Гейзенберга (1927 г.)
- 40. Для энергии и
- 41. х Соотношение неопределенностей получено при одновременном использовании классических
- 42. х Соотношение неопределенностей указывает, в какой мере, возможно,
- 43. хИз этого соотношения следует, что чем больше
- 44. хт.е. не будет сказываться при всех скоростях,
- 45. хПредположим, что пучок электронов движется вдоль оси
- 46. хТ.о., положение электрона может быть определено с
- 47. х Применим соотношение неопределенностей к электрону, двигающемуся в
- 48. х Используя законы классической физики, можно показать, что
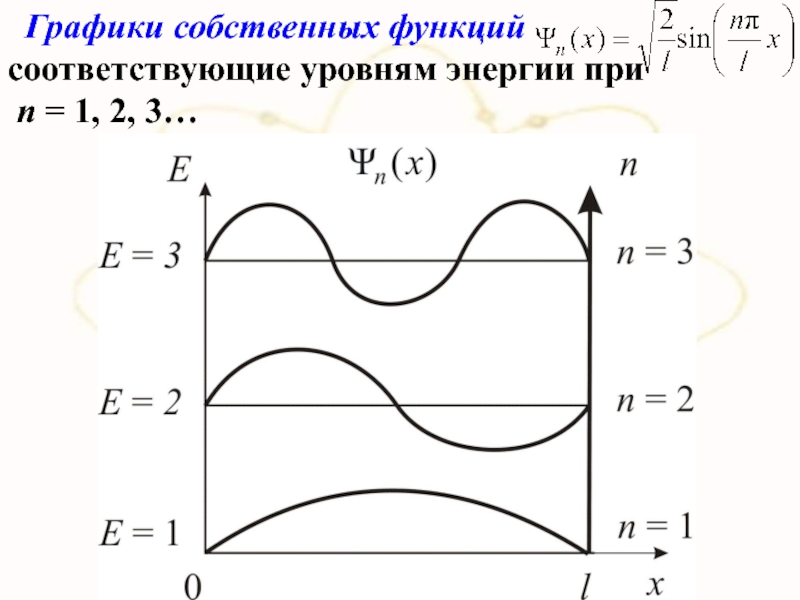
- 49. х4.2. Понятие о волновой функции Интенсивность волн
- 50. х Необходимость вероятностного подхода к описанию микрочастиц, является
- 51. х Чтобы устранить эти трудности немецкий физик М.
- 52. хВ квантовой механике состояние частицы описывается принципиально
- 53. х Величина |Ψ2|=dW/dV (квадрат модуля Ψ – функции)
- 54. Вероятность найти частицу в момент
- 55. хгде данный интеграл вычисляется по всему бесконечному
- 56. Чтобы волновая функция являлась объективной характеристикой состояния
- 57. х Волновая функция удовлетворяет принципу суперпозиции: если система
- 58. х Сложение волновых функций (амплитуд вероятностей определяемых квадратами
- 59. х4.3. Уравнение Шредингера Толкование волн де Бройля
- 60. х Основное уравнение должно быть уравнением относительно
- 61. хШредингер Эрвин (1887 – 1961) – австрийский
- 62. х Уравнение Шредингера не выводится, а постулируется. Правильность
- 63. х Уравнение Шредингера в
- 64. х Если силовое поле, в котором движется частица
- 65. Важным частным случаем общего уравнения
- 66. Уравнение Шредингера для стационарных состояний
- 67. ЭрвинШрёдингер(1887-1961)Любое движениемикрочастиц можноуподобить движениюособых волн
- 68. Тема 5. ДВИЖЕНИЕ СВОБОДНОЙ ЧАСТИЦЫ ВОДНОМЕРНОЙ ПОТЕНЦИАЛЬНОЙ
- 69. 5.1. Движение свободной частицы х Свободная частица –
- 70. х Прямой подстановкой можно убедиться в том, что
- 71. х Из выражения (2) следует, что зависимость энергии
- 72. хт.е. все положения свободной частицы являются равновероятностными. Таким
- 73. Проведем качественный анализ решений уравнения Шредингера, применительно
- 74. х Такая яма описывается потенциальной энергией видагде l
- 75. х Уравнение Шредингера для стационарных состояний в случае одномерной задачи запишется в виде: (3)
- 76. х По условию задачи (бесконечно высокие «стенки»), частица
- 77. х В пределах «ямы» (0
- 78. хОтсюда следует, что: (6)где n = 1,
- 79. х Квантовые значения энергии En называется уровнями энергии,
- 80. х Найдем собственные функции: Постоянную интегрирования А найдем
- 81. Графики собственных функций соответствующие уровням энергии при п = 1, 2, 3…
- 82. х Плотность вероятности |Ψ(x)|2 обнаружения
- 83. хИз выражения следует, что энергетический интервал между
- 84. Если же размеры ямы соизмеримы с размерами
- 85. х5.3. Гармонический осциллятор Гармоническим осциллятором называют частицу,
- 86. (а)(б). В точках с координатами –x0 и +x0,
- 87. х Гармонический осциллятор в квантовой механике - квантовый
- 88. х ΔEn= ω и
- 89. х В квантовой механике вычисляется вероятность различных переходов
- 90. хПлотность вероятности нахождения частицы |Ψ|2=Ψ∙Ψ*При n = 2 в середине ямы частицы быть не может.
- 91. х Таким образом, энергия гармонического осциллятора изменяется только
- 92. Кроме того, квантово – механический расчет показывает,
- 93. х5.4. Прохождение частиц сквозь потенциальный барьер. Туннельный
- 94. х При E < U имеется также отличная
- 95. х Уравнение Шредингера для состояний для каждой их
- 96. х Учитывая значение q и то, что А1
- 97. х1. В области 1 плоская волна де
- 98. Таким образом, квантовая механика приводит
- 99. х Коэффициент прозрачности для барьера прямоугольной формыДля барьера произвольной формы
- 100. х Прохождение частицы сквозь ,барьер можно пояснить соотношением
- 101. С классической точки зрения прохождение частицы сквозь
- 102. Основы теории туннельных переходов заложены работами
- 103. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Тема 3. ВОЛНОВЫЕ СВОЙСТВА
МИКРОЧАСТИЦ ВЕЩЕСТВА
3.1. Гипотеза де Бройля
3.2.
Дифракция электронов
Слайд 23.1. Гипотеза де Бройля
х
Появилась необходимость пересмотра основ квантовой теории
и представлений о природе микрочастиц (электронов, протонов и т.п.). Возник
вопрос о том, насколько исчерпывающим является представление электрона в виде малой механической частицы, характеризующейся определенными координатами и определенной скоростью.Мы уже знаем, что в оптических явлениях наблюдается своеобразный дуализм.
Наряду с явлениями дифракции, интерференции (волновыми явлениями) наблюдаются и явления, характеризующие корпускулярную природу света (фотоэффект, эффект Комптона).
Слайд 3х
В 1924 г. Луи де Бройль выдвинул смелую гипотезу, что
дуализм не является особенностью только оптических явлений, а имеет универсальный
характер:частицы вещества также обладают волновыми свойствами.
Слайд 4х
Луи де Бройль (1892 – 1987), французский физик, удостоенный Нобелевской
премии 1929 г. по физике за открытие волновой природы электрона.
В 1923 г., распространив идею А.Эйнштейна о двойственной природесвета на вещество, предположил, что поток материальных частиц должен обладать и волновыми свойствами, связанными с их массой и энергией (волны де Бройля). Экспериментальное подтверждение этой идеи было получено в 1927 в опытах по дифракции электронов в кристаллах, а позже она получила практическое применение при разработке магнитных линз для электронного микроскопа. Концепцию де Бройля о корпускулярно-волновом дуализме использовал Э.Шредингер при создании волновой механики.
Слайд 5х
«В оптике, – писал де Бройль, – в течение столетия
слишком пренебрегали корпускулярным способом рассмотрения по сравнению с волновым; не
делалась ли в теории вещества обратная ошибка?»Допуская, что частицы вещества наряду с корпускулярными свойствами имеют также и волновые, де Бройль перенес на случай частиц вещества те же правила перехода от одной картины к другой, какие справедливы в случае света.
Слайд 6х
Если фотон обладает энергией E=hv и импульсом p=h/λ, то и
частица (например, электрон), движущаяся с некоторой скоростью, обладает волновыми свойствами,
т.е. движение частицы можно рассматривать как движение волны.Слайд 7 Согласно квантовой механике, свободное движение частицы с массой
m и импульсом p=mυ (где υ – скорость частицы) можно
представить как плоскую монохроматическую волну (волну де Бройля) с длиной волныПоскольку кинетическая энергия сравнительно медленно движущейся частицы , то длину волны можно выразить через энергию:
Слайд 8х
При взаимодействии частицы с некоторым объектом -
с кристаллом, молекулой и т.п. – её энергия меняется.
Соответственно, меняется характер распространения связанной с частицей волны, причём это происходит согласно принципам, общим для всех волновых явлений. Поэтому, основные геометрические закономерности дифракции частиц, ничем не отличаются от закономерностей дифракции любых волн.
Слайд 9х
Гипотеза де Бройля была революционной, даже
для того революционного в науке времени. Однако,
она вскоре была подтверждена многими экспериментами.Слайд 10х
3.2. Дифракция частиц
Дифракция частиц - рассеяние микрочастиц (электронов, нейтронов,
атомов и т.п.) кристаллами или молекулами жидкостей и газов, при
котором из начального пучка частиц данного типа возникают дополнительно отклонённые пучки этих частиц.Направление и интенсивность таких отклонённых пучков зависят от строения рассеивающего объекта.
Слайд 11х
Первым опытом по дифракции частиц, блестяще подтвердившим исходную идею квантовой
механики – корпускулярно-волновой дуализм, явился опыт американских физиков К. Дэвиссона
и Л. Джермера, проведенный в 1927 по дифракции электронов на монокристаллах никеля.Опыты по дифракции частиц
и их квантовомеханическая интерпретация.
Слайд 12"Некоторые исследователи -
Дэвисон и Джермер и молодой Томпсон -
приступили к
выполнению опытов,
за которые ещё несколько лет назад
их бы поместили
в
психиатрическую лечебницуСлайд 14Эти опыты показали, что в
определенных условиях свободные
электроны проявляют
свойства волн -
д и ф р а к ц
и ю.Слайд 15Ni монокристалл
пики дифракции
поток электронов
В опыте Дэвиссона и Джермера при «отражении»
электронов от поверхности кристалла никеля при определённых углах отражения возникали
максимумы.Слайд 16 Эти максимумы отражённых пучков электронов соответствовали условию Вульфа – Брэггов
:
и их появление не могло быть объяснено никаким
другим путём, кроме как на основе представлений о волнах и их дифракции; таким образом, волновые свойства частиц – электронов – были доказаны экспериментом.
Слайд 17х
При высоких ускоряющих напряжениях (десятках кВ) электроны приобретают достаточную кинетическую
энергию, чтобы проникать сквозь тонкие плёнки вещества (толщиной порядка 10–5
см, т. е. тысячи Å).Тогда возникает так называемая дифракция быстрых электронов на прохождение, которую на поликристаллических плёнках алюминия и золота впервые исследовали английский учёный Дж. Дж. Томсон и советский физик П. С. Тартаковский.
Слайд 18 В 1949 г. советские ученые Л.М. Биберман, Н.Г. Сушкин, В.А.
Фабрикант поставили такой же опыт, но интенсивность электронного пучка была
настолько слабой, что электроны проходили через прибор практически поодиночке. Однако картина после длительной экспозиции была точно такой же. Т.е. было доказано, что волновыми свойствами обладает каждый отдельный электрон.х
Слайд 19х
Вскоре после этого удалось наблюдать и явления дифракции атомов и
даже молекул!
Атомам с массой μ, находящимся в газообразном состоянии
в сосуде при абсолютной температуре Т, соответствует длина волны: где k –постоянная Больцмана,
E=2/3kT - средняя кинетическая энергия атома
Слайд 20х
Для лёгких атомов и молекул (H2,
Не), и температур в сотни градусов Кельвина, длина волны также
составляет около 1 Å. Дифрагирующие атомы или молекулы практически не проникают в глубь кристалла, поэтому можно считать, что их дифракция происходит при рассеянии от поверхности кристалла, т. е. как на плоской дифракционной решётке.Слайд 21х
Сформированный с помощью диафрагм молекулярный или атомный пучок, направляют на
кристалл и тем или иным способом фиксируют «отражённые» дифракционные пучки.
Таким путём немецкие учёные О. Штерн и И. Эстерман, а также др. исследователи на рубеже 30-х гг. наблюдали дифракцию атомных и молекулярных пучков
Слайд 22х
Позже наблюдалась дифракция протонов, а также дифракция нейтронов, получившая широкое
распространение как один из методов исследования структуры вещества.
Так было доказано экспериментально, что волновые свойства присущи всем без исключения микрочастицам. Слайд 27х
Дифракция частиц, сыгравшая в своё время столь большую роль в
установлении двойственной природы материи – корпускулярно-волнового дуализма (и тем самым
послужившая экспериментальным обоснованием квантовой механики), давно уже стала одним из главных рабочих методов для изучения строения вещества.На дифракции частиц основаны два важных современных метода анализа атомной структуры вещества – электронография и нейтронография.
Слайд 28х
3.3. Корпускулярно- волновой
дуализм микрочастиц вещества
Итак, микрочастицы обладают необычайными свойствами.
Микрочастицы – это элементарные частицы (электроны, протоны, нейтроны и т.д.),
а также сложные частицы, образованные из небольшого числа элементарных (пока неделимых) частиц (атомы, молекулы, ядра атомов). Называя эти микрочастицы частицами, мы подчеркиваем только одну сторону, правильнее было бы назвать «частица – волна».Слайд 29 Микрочастицы не способны непосредственно воздействовать на наши органы чувств
– ни видеть, ни осязать их нельзя.
Ничего подобного в
осязаемом нами мире не существует. «Раз поведение атомов так не похоже на наш обыденный опыт, то к нему очень трудно привыкнуть, потому что весь непосредственный опыт человека, вся его интуиция – все прилагается к крупным телам». Мы знаем, что будет с большим предметом; но именно так микрочастицы не поступают! Поэтому, изучая их приходится прибегать к различного рода абстракциям, напрягать воображение и не пытаться связать их с нашим непосредственным опытом.
х
Слайд 30х
В доквантовой физике понять - значить составить себе наглядный образ
объекта или процесса. В квантовой физике так рассуждать нельзя.
Всякая
наглядная модель будет действовать по классическим законам и поэтому непригодна для представления квантовых процессов. Например, вращение электрона по орбите вокруг атома – такое представление. Это дань классической физике и не соответствует истинному положению вещей, не соответствует квантовым законам. Слайд 31х
Рассмотренные нами волны де Бройля не являются электромагнитными, это волны
особой природы.
Вычислим дебройлевскую длину волны мячика массой 0,20 кг, движущегося
со скоростью 15 м/с. Это чрезвычайно малая длина волны.
Даже при крайне низких скоростях, скажем 10–4м/с, дебройлевская длина волны составляла бы примерно 10–29м.
Слайд 32х
Дебройлевская длина волны обычного тела слишком мала, чтобы ее можно
было обнаружить и измерить.
Дело в том, что типичные волновые
свойства – интерференция и дифракция – проявляются только тогда, когда размеры предметов или щелей сравнимы по своей величине с длиной волны. Но нам не известны предметы и щели, на которых могли бы дифрагировать волны с длиной волны 10–30м, поэтому волновые свойства обычных тел обнаружить не удается.
Слайд 33х
Другое дело, если речь идет об элементарных частицах типа электронов.
Т.к. масса входит в знаменатель формулы
очень малой массе соответствует
большая длина волны.Определим дебройлевскую длину волны электрона, ускоренного разностью потенциалов 100 В.
м/с
откуда
Слайд 34х
Из приведенного примера видно, что электрон может соответствовать длине волны
порядка 10–10 м.
Хотя это очень короткие волны,
их можно обнаружить экспериментально: межатомные расстояния в кристалле того же порядка величины (10–10м.) и регулярно расположенные атомы кристалла можно использовать в качестве дифракционной решетки, как в случае рентгеновского излучения. Слайд 35Тема 4. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
4.1. Соотношение неопределенности
Гейзенберга
4.2. Понятие о
волновой функции
х
4.3. Уравнение Шредингера
Слайд 36х
4.1. Соотношение неопределенности
Гейзенберга
Согласно двойственной корпускулярно-волновой природе частиц вещества,
для описания микрочастиц используются то волновые, то корпускулярные представления.
Поэтому
приписывать им все свойства частиц и все свойства волн нельзя. Естественно, что необходимо внести некоторые ограничения в применении к объектам микромира понятий классической механики.
Слайд 37 Корпускулярно-волновая двойственность свойств частиц, изучаемых в квантовой механике, приводит
к тому, что оказывается невозможным одновременно характеризовать частицу ее положением
в пространстве (координатами) и скоростью (или импульсом). Так, например, электрон (и любая другая микрочастица) не может иметь одновременно точных значений координаты x и импульса px. Неопределенности значений x и px удовлетворяют соотношениюх
где h – постоянная Планка.
Слайд 38х
Из уравнения следует, что чем меньше неопределенность одной величины (x
или px), тем больше неопределенность другой. Возможно, такое состояние, в
котором одна их переменных имеет точное значение (Δx=0), другая переменная при этом оказывается совершенно неопределенной (Δp→∞ – ее неопределенность равна бесконечности), и наоборот. Таким образом, для микрочастицы не существует состояний, в которых ее координаты и импульс имели бы одновременно точные значения.Отсюда вытекает и фактическая невозможность одновременного с любой наперед заданной точностью изменить координату и импульс микрообъекта.
Слайд 40
Для энергии и времени также справедливо
соотношение неопределенностей
х
это соотношение означает, что определение энергии с точностью ΔE
должно занять интервал времени, равный, по меньшей мере Слайд 41х
Соотношение неопределенностей получено при одновременном использовании классических характеристик движения частицы
(координаты, импульса) и наличии у нее волновых свойств.
Т.к. в
классической механике принимается, что измерение координаты и импульса может быть произведено с любой точностью, то соотношение неопределенностей являются квантовым ограничением применимости классической механике к микрообъектам.
Слайд 42х
Соотношение неопределенностей указывает, в какой мере, возможно, пользоваться понятиями классической
механики применительно к микрочастицам,
в частности, с какой степенью точности
можно говорить о траекториях микрочастиц.Движение по траектории характеризуется вполне определенными значениями координат и скорости в каждый момент времени.
Подставив вместо px произведение mυy, получим соотношение
Слайд 43х
Из этого соотношения следует, что чем больше масса частицы, тем
меньше неопределенность ее координаты и скорости, следовательно, с тем большей
точностью можно применять к этой частице понятие траектории.Так, например, уже для пылинки массой 10–12 кг и линейным размерами 10–6 м, координата которой определена с точностью до 0,01 ее размеров (Δx=10–18 м), неопределенность скорости,
Слайд 44х
т.е. не будет сказываться при всех скоростях, с которыми пылинка
может двигаться. Таким образом, для макроскопических тел их волновые свойства
не играют ни какой роли; координаты и скорости могут быть измерены достаточно точно. Это означает, что для описания движения макротел с абсолютной достоверностью можно пользоваться законами классической механики.Слайд 45х
Предположим, что пучок электронов движется вдоль оси x со скоростью
υ=108 м/с, определяемой с точностью до 0,01 (Δυx≈104 м/с). Какова
точность определения координаты электрона? Получим:Слайд 46х
Т.о., положение электрона может быть определено с точностью до тысячных
долей миллиметра. Такая точность достаточна, чтобы можно было говорить о
движении электронов по определенной траектории, иными словами, описывать их движения законами классической механики.Слайд 47х
Применим соотношение неопределенностей к электрону, двигающемуся в атоме водорода.
Допустим,
что неопределенность координаты электрона Δx≈10–10 м (порядка размеров самого атома),
тогда,Слайд 48х
Используя законы классической физики, можно показать, что при движении электрона
вокруг ядра по круговой орбите радиуса
0,5∙10–10 м
его скорость υ≈2,3∙106 м/с. Таким образом, неопределенность скорости в несколько раз больше самой скорости. Очевидно, что в данном случае нельзя говорить о движении электронов в атоме по определенной траектории, иными словами, для описания движения электронов в атоме нельзя пользоваться законами классической физики.
Слайд 49х
4.2. Понятие о волновой функции
Интенсивность волн де Бройля в
данной точке пространства связана с числом частиц, попавших в эту
точку, о чем говорили все опыты по дифракции частиц. Поэтому волновые свойства микрочастиц требуют статистического (вероятностного) подхода к их описанию.Слайд 50х
Необходимость вероятностного подхода к описанию микрочастиц, является важнейшей отличительной особенностью
квантовой теории.
Можно ли волны де Бройля истолковывать как волны
вероятности, т.е. считать, что вероятность обнаружить микрочастицу в различных точках пространства меняется по волновому закону? Такое толкование волн де Бройля уже неверно, хотя бы потому, что тогда вероятность обнаружить частицу в некоторых точках пространства может быть отрицательна, что не имеет смысла.
Слайд 51х
Чтобы устранить эти трудности немецкий физик М. Борн в 1926
г. предположил, что по волновому закону меняется не сама вероятность,
а величина, названная амплитудой вероятности и обозначаемаяΨ(х, y, z, t).
Эту величину называют также волновой функцией (или Ψ – функцией).
Слайд 52х
В квантовой механике состояние частицы описывается принципиально по-новому –
с
помощью волновой функции, которая является основным носителем информации об их
корпускулярных и волновых свойствах.Вероятность нахождения частицы в объеме V равна:
Слайд 53х
Величина |Ψ2|=dW/dV (квадрат модуля Ψ – функции) имеет смысл плотности
вероятности, т.е. определяет вероятность нахождения частицы в единице объема в
окрестности точки, имеющей x, y, z.Таким образом, физический смысл имеет не сама Ψ – функция, а квадрат ее модуля |Ψ2|, которым определяется интенсивность волн де Бройля.
Слайд 54 Вероятность найти частицу в момент времени t в
конечном объеме V, согласно теореме о сложении вероятностей, равна:
х
Т.к.
|Ψ|2dυ определяется как вероятность, то необходимо волновую функцию Ψ представить так, чтобы вероятность достоверного события обращалась в единицу, если за объем V принять бесконечный объем всего пространства. Это означает, что при данном условии частица должна находиться где-то в пространстве.
Слайд 55х
где данный интеграл вычисляется по всему бесконечному пространству, т.е. по
координатам x, y, z от –∞ до ∞.
Таким
образом, условие нормировки говорит об объективном существовании частицы во времени и пространстве. Условия нормировки вероятностей:
Слайд 56 Чтобы волновая функция являлась объективной характеристикой состояния микрочастицы, она должна
удовлетворять ряду ограничительных условий.
Функция Ψ, характеризующая вероятность
обнаружить действия микрочастицы в элементе объема, должна быть:конечной (вероятность не может быть больше единицы);
однозначной (вероятность не может быть неоднозначной величиной);
непрерывной (вероятность не может меняться скачком).
х
Слайд 57х
Волновая функция удовлетворяет принципу суперпозиции: если система может находиться в
различных состояниях, описываемых волновыми функциями Ψ1, Ψ2, … Ψn, то
она может находиться в состоянии, описываемом линейной комбинацией этих функцийгде Cn (n = 1, 2, 3…) – произвольные, комплексные числа.
Слайд 58х
Сложение волновых функций (амплитуд вероятностей определяемых квадратами модулей волновых функций)
принципиально отличает квантовую теорию от классической статической теории, в которой
для независимых событий справедлива теорема сложения вероятностей.Слайд 59х
4.3. Уравнение Шредингера
Толкование волн де Бройля и соотношение неопределенностей
Гейзенберга привели к выводу, что уравнением движения в квантовой механике,
описывающей движение микрочастиц в различных силовых полях, должно быть уравнение, из которого бы вытекали наблюдаемые на опыте волновые свойства частиц.Слайд 60х
Основное уравнение должно быть уравнением относительно волновой функции Ψ(х,
y, z, t), т.к. именно величина |Ψ|2, осуществляет вероятность пребывания
частицы в момент времени t в объеме dV, т.е. в области с координатами x и x+dx, y, и y+dy, z и z+dz.Т.к. искомое уравнение должно учитывать волновые свойства частиц, то оно должно быть волновым уравнением, подобно уравнению, описывающему электромагнитные волны.
Основное уравнение нерелятивистской квантовой механики сформулировано в 1926 г. Э.Шредингером.
Слайд 61х
Шредингер Эрвин (1887 – 1961) – австрийский физик-теоретик, один из
создателей квантовой механики. Основные работы в области статистической физики, квантовой
теории, квантовой механики, общей теории относительности, биофизики.Разработал теорию движения микрочастиц – волновую механику, построил квантовую теорию возмущений – приближенный метод в квантовой механике. За создание волновой механики удостоен Нобелевской премии.
Слайд 62х
Уравнение Шредингера не выводится, а постулируется.
Правильность этого уравнения подтверждается
согласием с опытом получаемых с его помощью результатов, что в
свою очередь, придает ему характер закона природы.Слайд 63х
Уравнение Шредингера в общем виде записывается
так:
где
- постоянная Планка, m – масса частицы.
– оператор Лапласа
i – мнимая единица,
U(x, y, z, t) – потенциальная функция частицы в силовом поле, в котором она движется,
Ψ – искомая волновая функция.
Слайд 64х
Если силовое поле, в котором движется частица потенциально, то функция
U не зависит явно от времени и имеет смысл потенциальной
энергии.В этом случае решение уравнения Шредингера распадается на два сомножителя, один из которых зависит только от координаты, а другой – только от времени.
Здесь E – полная энергия частицы, которая в случае стационарного поля остается постоянной.
Слайд 65 Важным частным случаем общего уравнения Шрёдингера , является
уравнение Шрёдингера для стационарных состояний, в котором исключена зависимость Ψ
от времени, и, поэтому, значения энергии этих состояний являются фиксированными (не изменяются со временем).В этом случае поле, в котором движется частица, является стационарным.Слайд 68Тема 5. ДВИЖЕНИЕ СВОБОДНОЙ ЧАСТИЦЫ В
ОДНОМЕРНОЙ ПОТЕНЦИАЛЬНОЙ ЯМЕ
5.1. Движение
свободной частицы
5.2. Частица в одномерной прямоугольной
яме с бесконечными внешними «стенками»
5.3.
Гармонический осцилляторх
5.4. Прохождение частиц сквозь
потенциальный барьер. Туннельный эффект
Слайд 695.1. Движение свободной частицы
х
Свободная частица – частица, движущаяся в
отсутствие внешних полей.
Т.к. на свободную частицу (пусть она движется
вдоль оси x) силы не действуют, то потенциальная энергия частицы U(x)=const и ее можно принять равной нулю: (U=0) Тогда полная энергия частицы совпадает с ее кинетической энергией.
В таком случае уравнение Шредингера для стационарных состояний примет вид
(1)
Слайд 70х
Прямой подстановкой можно убедиться в том, что частным решением уравнения
(1) является функция
где A=const и k=const, с собственным значением
энергии: (2)
Слайд 71х
Из выражения (2) следует, что зависимость энергии от импульса
оказывается
обычной для нерелятивистских частиц.
Следовательно, энергия свободной частицы может принимать
любые значения (т.к. число может принимать любые значения), т.е. ее энергетический спектр является непрерывным. Слайд 72х
т.е. все положения свободной частицы являются равновероятностными.
Таким образом, свободная частица
описывается плоской монохроматической волной де Бройля.
Этому способствует не зависящая
от времени плотность вероятности обнаружения частицы в данной точке пространства.Слайд 73 Проведем качественный анализ решений уравнения Шредингера, применительно к частице в
яме с бесконечно высокими «стенками».
5.2. Частица в одномерной прямоугольной
яме с
бесконечными внешними «стенками» Слайд 74х
Такая яма описывается потенциальной энергией вида
где l – ширина «ямы»,
а энергия отсчитывается от ее дна. (для простоты принимая, что
частица движется вдоль оси x)Слайд 75х
Уравнение Шредингера для стационарных состояний в случае одномерной задачи запишется
в виде:
(3)
Слайд 76х
По условию задачи (бесконечно высокие «стенки»), частица не проникает за
пределы «ямы», поэтому вероятность ее обнаружения, (а следовательно, и волновая
функция) за пределами «ямы» равна нулю.На границах ямы волновая функция также должна обращаться в нуль. Следовательно, граничные условия в таком случае имеют вид
(4)
Слайд 77х
В пределах «ямы» (0 ≤ x ≤
l) уравнение Шредингера (3) сведется к уравнению
(5)
где
Общее решение дифференциального
уравнения (5) Уравнение Ψ(l) = A sin kl = 0 выполняется только при
Слайд 78х
Отсюда следует,
что:
(6)
где n = 1, 2, 3…
Т.е. стационарное уравнение Шредингера описывающее движение частицы в «потенциальной
яме» с бесконечно высокими «стенками», удовлетворяется только при собственных значениях En, зависящих от целого числа n.Следовательно, энергия En частицы в «потенциальной яме» с бесконечно высокими «стенками» принимает лишь определенные дискретные значения, т.е. квантуется.
Слайд 79х
Квантовые значения энергии En называется уровнями энергии, а число п,
определяющее энергетические уровни - главным квантовым числом.
Таким образом, микрочастица
в «потенциальной яме» с бесконечно высокими «стенками» может находиться только на определенном энергетическом уровне En, или как говорят, частица находится в квантовом состоянии п. Слайд 80х
Найдем собственные функции:
Постоянную интегрирования А найдем из условия нормировки:
В
результате интегрирования получим
Соответственные функции будут иметь вид:
где
n = 1, 2, 3…Слайд 82х
Плотность вероятности |Ψ(x)|2 обнаружения частицы на различных
расстояниях от «стенок» ямы для п = 1, 2,
3 В квантовом состоянии с п = 2 частица не может находиться в центре ямы, в то время как одинаково может пребывать в ее левой и правой частях.
Такое поведение частицы указывает на то, что представления о траекториях частицы в квантовой механике несостоятельны.
Слайд 83х
Из выражения
следует, что энергетический интервал между двумя соседними
условиями равен
Например, для электрона при размерах ямы l=10–10м (свободные
электроны в металле) ΔEn ≈ 10–35 n Дж ≈ 10–16 n Эв,
т.е. энергетические уровни расположены столь тесно, что спектр можно считать практически непрерывным.
Слайд 84 Если же размеры ямы соизмеримы с размерами стенки (l ≈
10–10 м), то для электрона
ΔEn ≈ 10–17 n Дж
≈ 10–2 n Эв, т.е. получаются явно дискретные значения энергии (линейчатый спектр).
Т.о., применение уравнения Шредингера к частице в «потенциальной яме» с бесконечно высокими “стенками” приводит к квантовым значениям энергии, в то время как классическая механика на энергию этой частицы лишних ограничений не накладывает.
х
Слайд 85х
5.3. Гармонический осциллятор
Гармоническим осциллятором называют частицу, совершающую одномерное движение
под действием квазиупругой силы F=kx.
Потенциальная энергия частицы
.
где
или
Слайд 86(а)
(б)
.
В точках с координатами –x0 и +x0, полная энергия равна
потенциальной энергии. Поэтому
с классической точки зрения частица не может выйти
за пределы области –x0 и +x0График потенциальной энергии частицы:
Слайд 87х
Гармонический осциллятор в квантовой механике - квантовый осциллятор - описывается
уравнением Шредингера:
Значения полной энергии осциллятора
где n = 0, 1, 2…
Слайд 88х
ΔEn= ω и
не зависит от
n.
называется нулевой энергией, т.е. при Т = 0К колебания атомов
в кристаллической решетке не прекращаются. Это означает что частица не может находиться на дне потенциальной ямы.
Минимальная
энергия
Слайд 89х
В квантовой механике вычисляется вероятность различных переходов квантовой системы из
одного состояния в другое. Для гармонического осциллятора возможны лишь переходы
между соседними уровнями. Условия, накладываемые на изменения квантовых чисел при переходах системы из одного состояния в другое, называются правилами отбора:
Слайд 90х
Плотность вероятности нахождения частицы
|Ψ|2=Ψ∙Ψ*
При n = 2 в середине
ямы частицы быть не может.
Слайд 91х
Таким образом, энергия гармонического осциллятора изменяется только порциями, т.е. квантуется
Причем
минимальная порция энергии
(Вспомним тепловые излучения, где энергия излучается квантами).
Кроме того например, при n = 2 в середине сосуда частицы быть не может. Это совершенно непонятно с классической точки зрения. Квантуется не только энергия, но и координата частицы! Слайд 92 Кроме того, квантово – механический расчет показывает, что частицу можно
обнаружить и за пределами ямы, т.е. в области с координатами
–x0 и +x0 , в то время как с классической точки зрения она не может выйти за пределы этой ямы.Слайд 93х
5.4. Прохождение частиц сквозь
потенциальный барьер. Туннельный эффект
Рассмотрим простейший
потенциальный барьер прямоугольной формы высоты U и шириной l для
одномерного (по оси х) движения частицы.Рисунок 5
При данных условиях задачи классическая частица, обладая энергией Е:
либо беспрепятственно пройдет под барьером,
либо отразится от него (E < U) и будет двигаться в обратную сторону, т.е. она не может проникнуть через барьер.
Слайд 94х
При E < U имеется также отличная от нуля вероятность,
что частица окажется в области x > l, т.е. проникнет
сквозь барьер.Такой вывод следует непосредственно из решения уравнения Шредингера, описывающего движение микрочастицы при данных условиях задачи.
Для микрочастицы же, даже при E > U, имеется отличная от нуля возможность, что частица отразится от барьера и будет двигаться в обратную сторону.
Слайд 95х
Уравнение Шредингера для состояний для каждой их выделенных областей имеет
вид:
Общее решение этих дифф. уравнений:
Здесь q = iβ –
мнимое число, Слайд 96х
Учитывая значение q и то, что А1 = 1, B3
= 0, получим решение уравнения Шредингера для трех областей в
следующем виде: В области 2 функция уже не соответствует плоским волнам, распространяющимся в обе стороны, поскольку показатели степени не мнимые а действительные
Слайд 97х
1. В области 1 плоская волна де Бройля.
2. Волновая функция
не равна нулю и внутри барьера, хотя уже не соответствует
плоским волнам де Бройля3. В области 3, если барьер не очень широк, будет опять иметь вид волн де Бройля с тем же импульсом, т.е. с той же частотой, но с меньшей амплитудой.
Качественный анализ функций Ψ1(x), Ψ2(x), Ψ3(x) показан на рис.
Слайд 98 Таким образом, квантовая механика приводит к принципиально новому
квантовому явлению -
туннельному эффекту,
в результате которого микрообъект
может пройти через барьер.Слайд 100х
Прохождение частицы сквозь ,барьер можно пояснить соотношением неопределенностей: Неопределенность импульса
на отрезке Δx = l составляет
Связанная с этим
разбросом в значении импульсаможет оказаться достаточной для того, чтобы полная энергия оказалась больше потенциальной.
кинетическая энергия
Слайд 101 С классической точки зрения прохождение частицы сквозь потенциальный барьер при
E < U невозможно, так как частица,
находясь в области барьера, должна была бы обладать отрицательной кинетической энергией.Туннельный эффект является специфическим квантовым эффектом.
Слайд 102 Основы теории туннельных переходов заложены работами
советских ученых
Л.И. Мандельштама и М.А. Леонтовича в 1928
г. Туннельное прохождение сквозь потенциальный барьер лежит в основе многих явлений:физики твердого тела (например, явления в контактном слое на границе двух полупроводников),
атомной и ядерной физики
(например, α-распад, протекание термоядерных реакций).